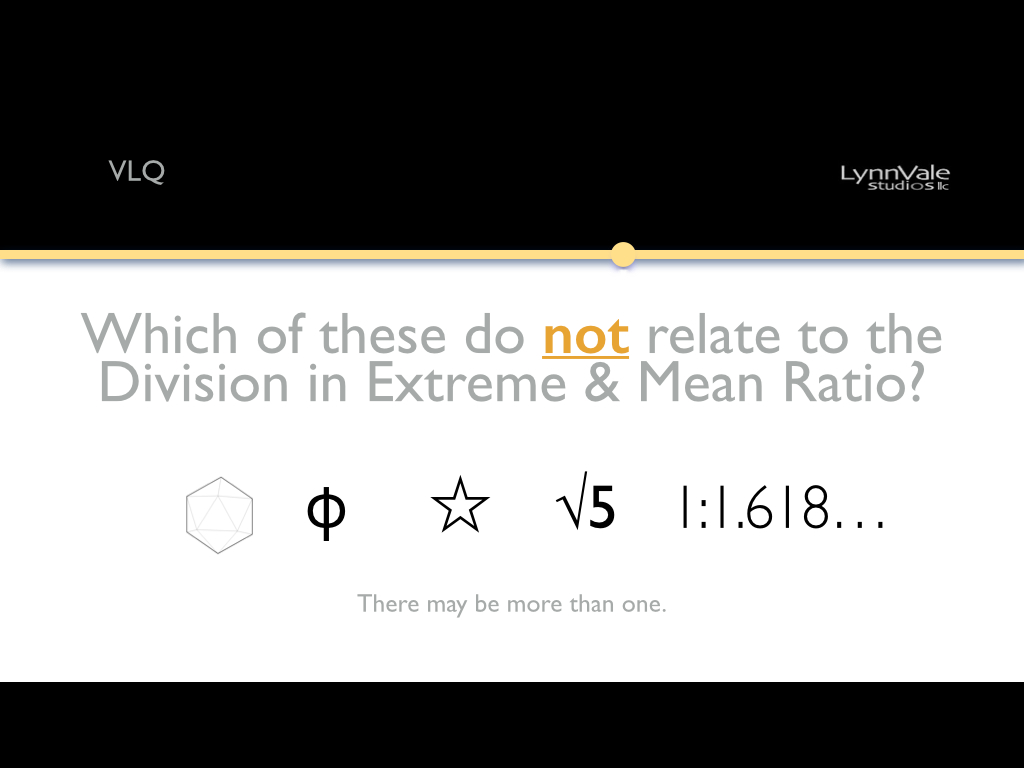
First, the Division in Extreme and Mean Ration (DEMR) is a proportional relationship discovered by Euclid * and documented in his book Elements around 300 BC. Simply put, the ratio follows: ac:ab = ab:bc. Diagram 1

In other words the whole relates back to the parts. If ab = 1 then bc = .618… (again an irrational number) totaling 1.618. Further, 1 ÷ 1.618… = .618… also irrational. ϕ is the math symbol for the number 1.618… in the same way π is the symbol for 3.14… So two (1.168 & ϕ) of the five options are related to the DEMR.
What if we add .618… to 1.618… (ϕ)? 1.618… + .618… = 2.236… which, if you have a calculator, is the √5. That’s 3 for five.
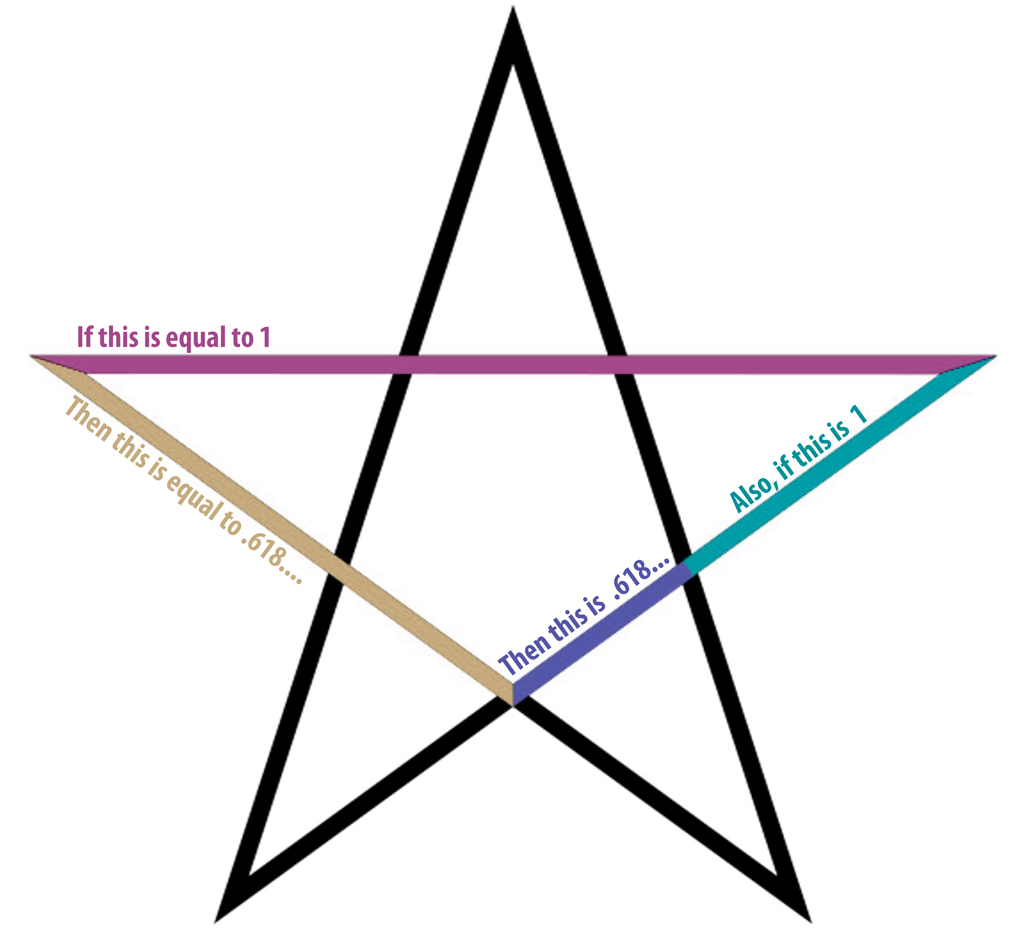
What about that star? Or, more appropriately, Pentagram. Diagram 2
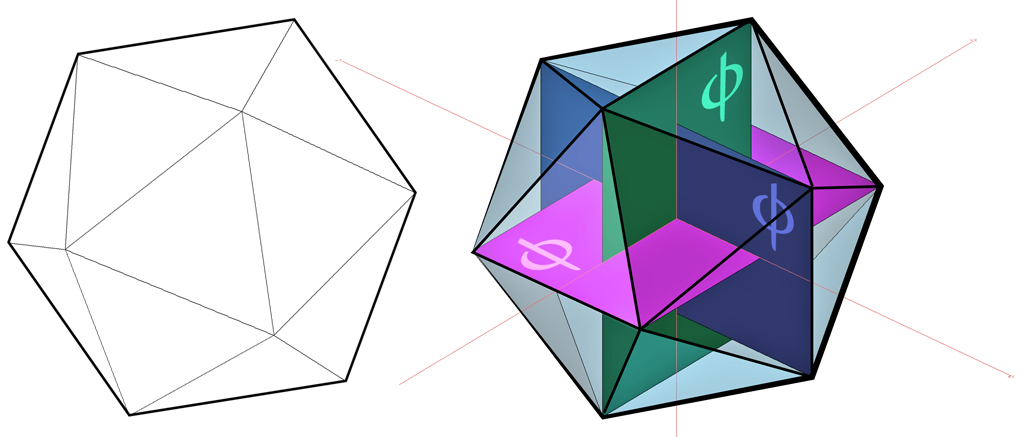
Well, that’s 4 out of 5. So what exactly is that first item to the left? It’s an Icosahedron. An Icosahedron is one of five Platonic Solids which are defined as polyhedron with all sides being regular polygons of the same size. The Icosahedron is composed of 20 equilateral triangles.
Time for a quick detour.
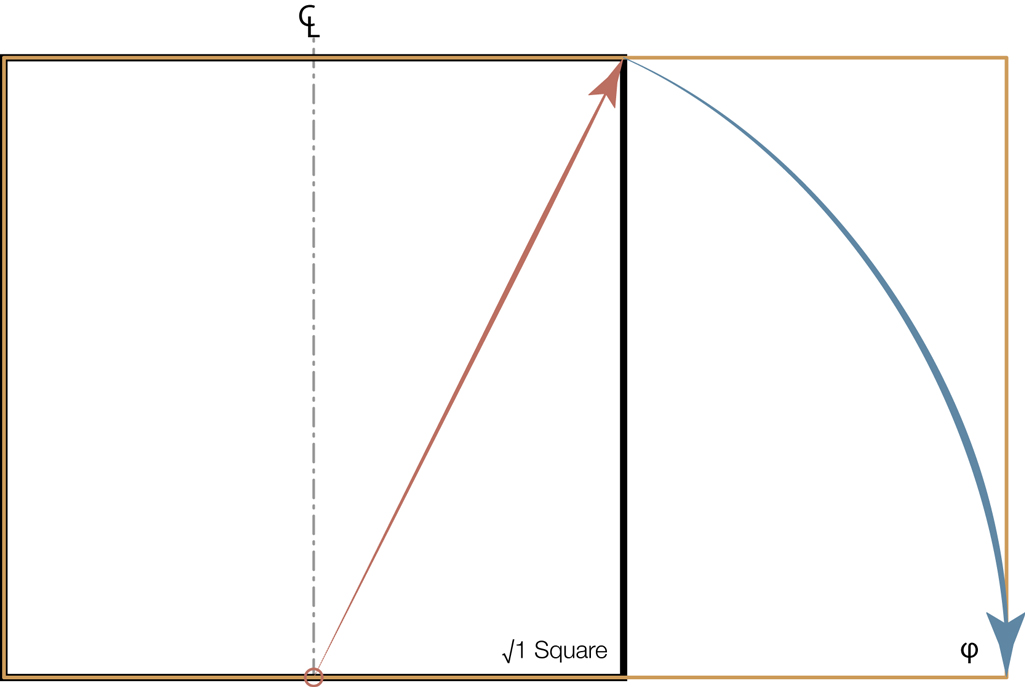
Let’s go back to our friend the square, divide it in half, draw a line from the bottom center to the upper right and then swing that line down to the base. Diagram 3 A square has the proportion of 1:1. The length added to the square from the compass swing is .618… As we know 1 + .618… = 1.618… so we have constructed a ϕ rectangle with the proportions 1:1.618…
Turns out that three ϕ rectangles fit perfectly within the Icosahedron. One each aligns with the x, y and z axes. Diagram 4
So all 5 of the above symbols and numbers relate to the Division in the Extreme and Mean Ratio. And, there’s a lot more to come…
* It’s likely that this concept was understood well before Euclid and that he is just the first to document it. We”ll look at this in more detail later.
