Geometry is the foundation of all painting.     

– Albrecht Dürer

There is another way to organize any rectangle in addition to the previous irrational rectangles.

Imagine a rectangle with a square scaled to the short side of the overall rectangle. Plate 1

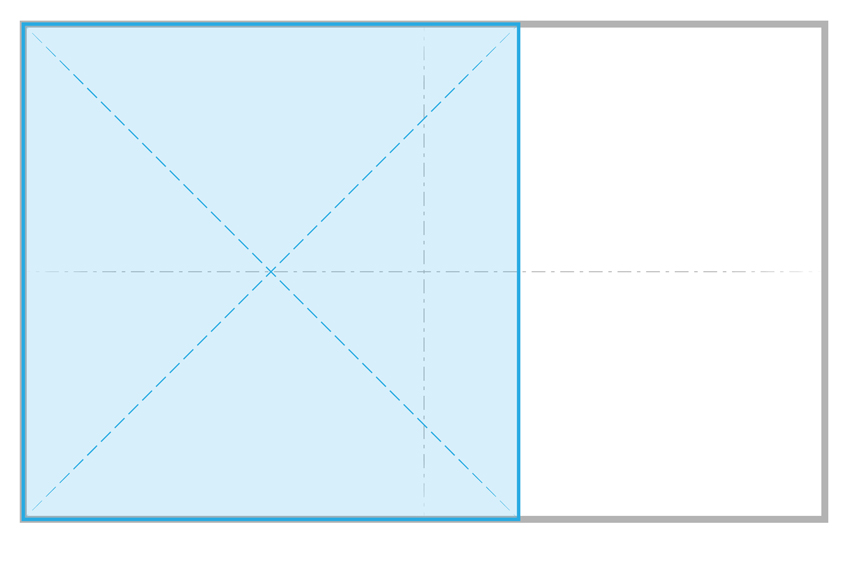
Now mirror that square about the centerline of the overall rectangle. This is Rabatment. Plate 2

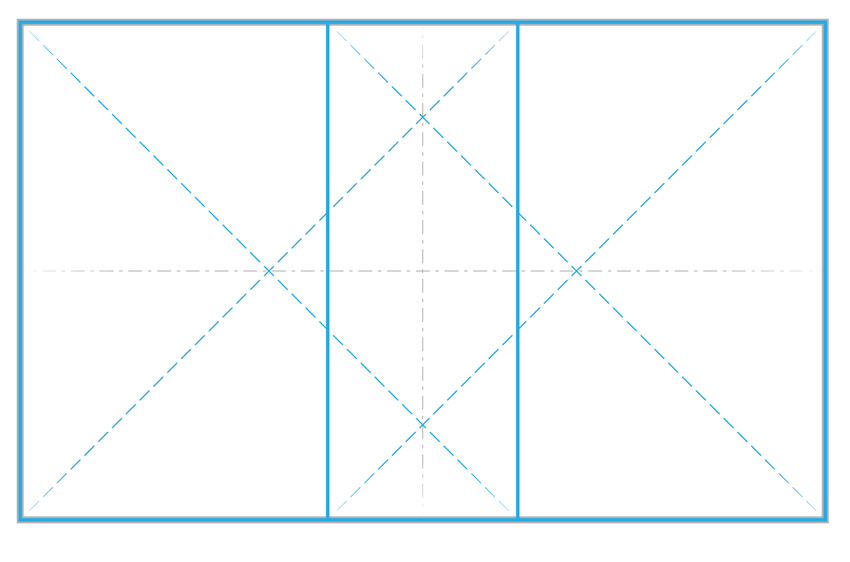
Remember the square is considered whole, unified and harmonious. Rabatment is a simple way to organize any rectangle. Please note that the 45° diagonals of each square are also implied.

Also note that the Primary Diagonal (Red Thick), Square Diagonal (Blue) and Reciprocal Diagonals (Red Thin) are equidistant to each other creating a radiating quality that is very useful in organizing spacial relationships in complex compositions. The Reciprocal diagonals are always 90º to the Primary Diagonal and the diagonal of the square is 45º which is half of 90º. Plate 3

 Rabatment is possible in any rectangle. Root rectangles and φ rectangles can also be employ Rebated Squares. This rectangle (above) has the φ aspect ratio.

This is ‘Saint Francis before the Sultan’ by Giotto di Bondone in 1325. The fresco is in the Basilica di Santa Croce in Florence, Italy. Here we can see the Rabated Squares. Plate 4

As seen in  ‘Triumph of Bacchus’ (by Michaelina Wautier) a complex composition can employ both rabatment and the topology of the parent rectangle.

We can also see the use of Rabated Squares in ‘A Dance to the Music of Time’ by Nicolas Poussin. Plate 5

Finally, we can see all of elements together. Plate 6

Mighty is geometry; joined with art, resistless.   

– Euripides