Topology: Part III
As we learned in the Topology: Part II post, one of the Primary Shapes is a Square. A square is a rectangle with the proportions 1:1. Primary shapes have their own organizing elements. A circle is defined by it’s radius. A triangle has three sides and three vertices. A rectangle has two vertical sides that are parallel and two horizontal sides which are parallel that meet at four vertices at a right angle (90°). A Rhombus is also a Quadrilateral but its sides do not meet at 90° at the vertices.
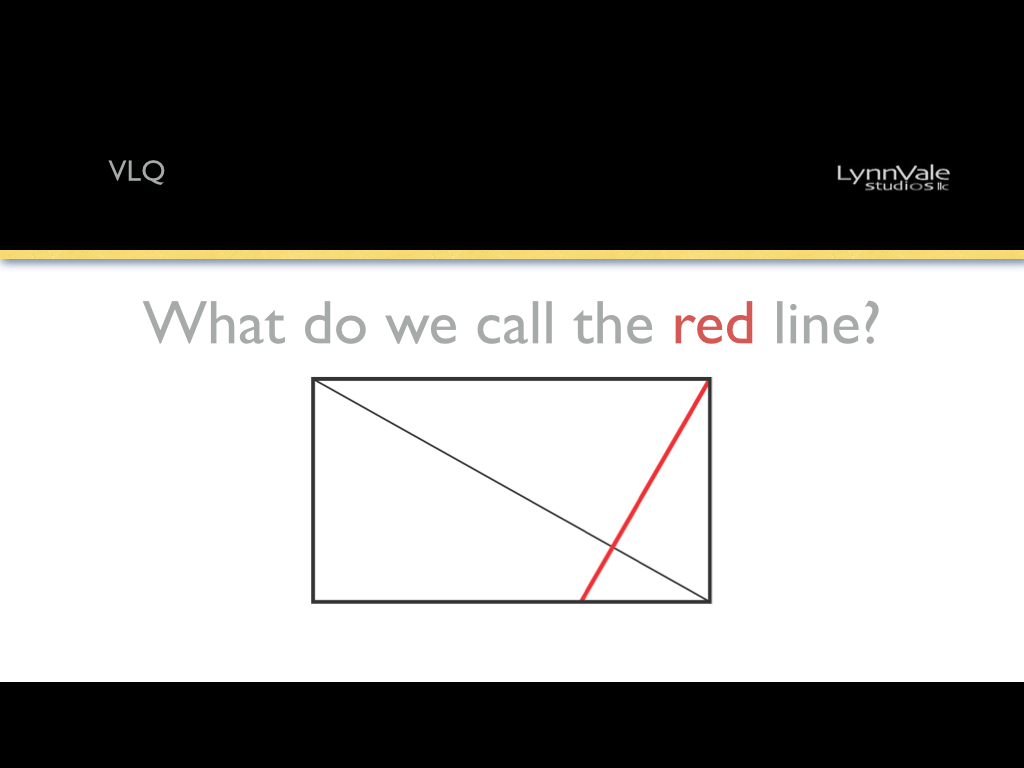
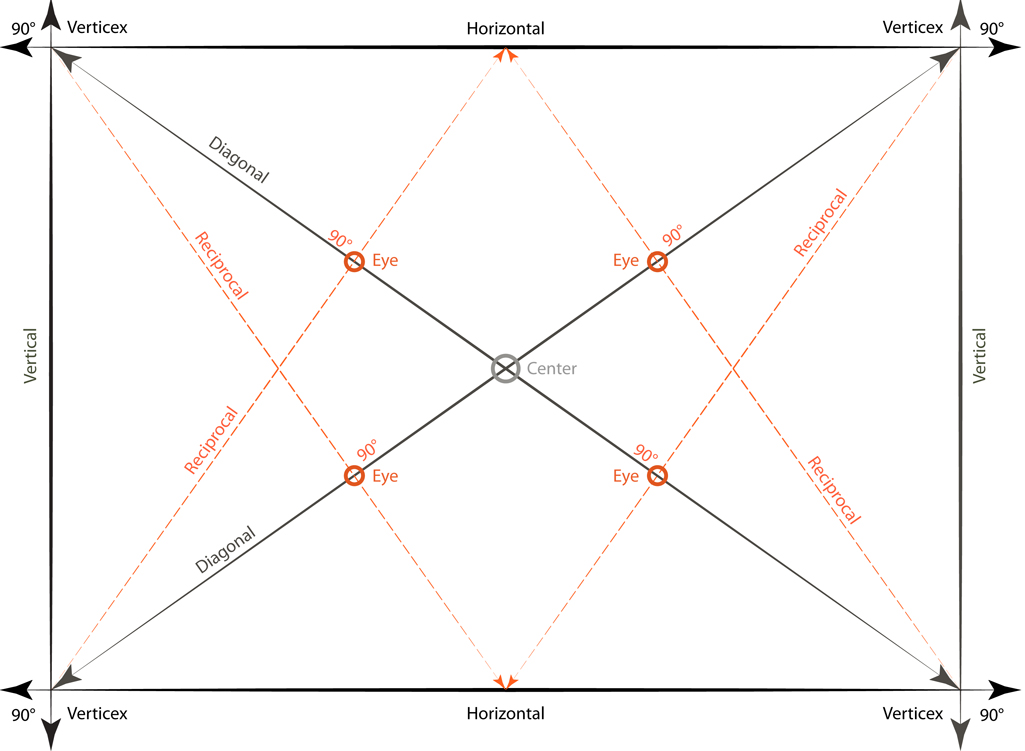
A rectangle also has two diagonals. One that goes from the lower left hand corner to the upper right hand corner and another that goes from the upper left hand corner to the lower right hand corner. Do you know their names?
In the diagram above we have a diagonal that starts at the upper left and ends at the lower right. The Red line starts at the upper right corner and intersects the diagonal at 90°. This is known (mathematically) as the Reciprocal. Diagram 1
So why does this matter to artists and designers? Well, if we draw a line from where the Reciprocal meets the bottom of the rectangle up to the top of the rectangle we get another rectangle (child) that shares the same proportions as the original rectangle (parent). Diagram 2
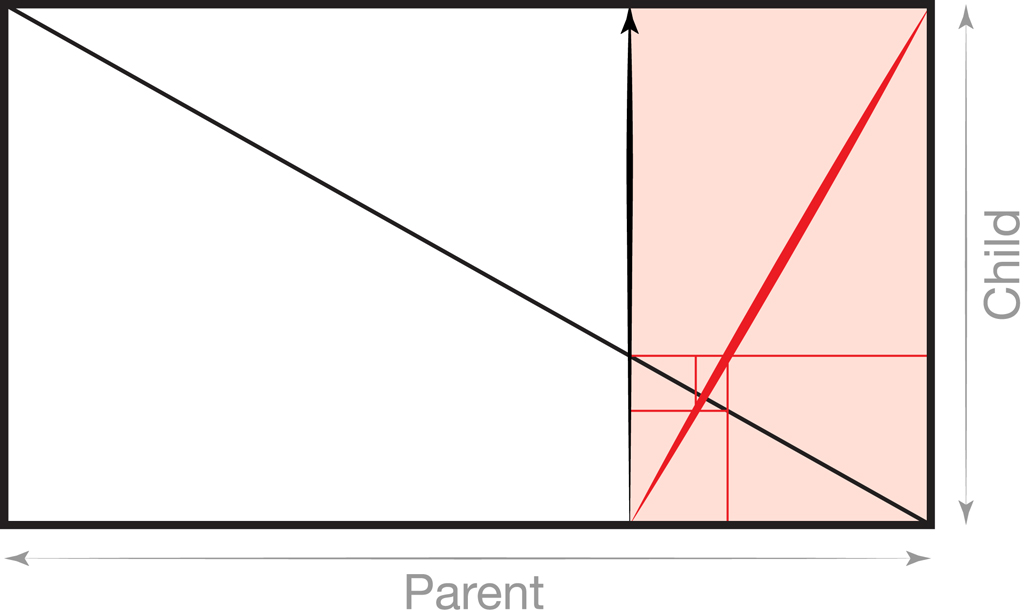
In other words, it Relates and it doesn’t end with one. The Reciprocal of the Parent becomes the Diagonal of the Child and a segment of the Diagonal becomes the new Reciprocal generation after generation. This is the case for all rectangles.
But, it turns out, some rectangles are more fun than others…
