And so we continue the introduction of Dynamic Symmetry from our understanding of the √2 rectangle.

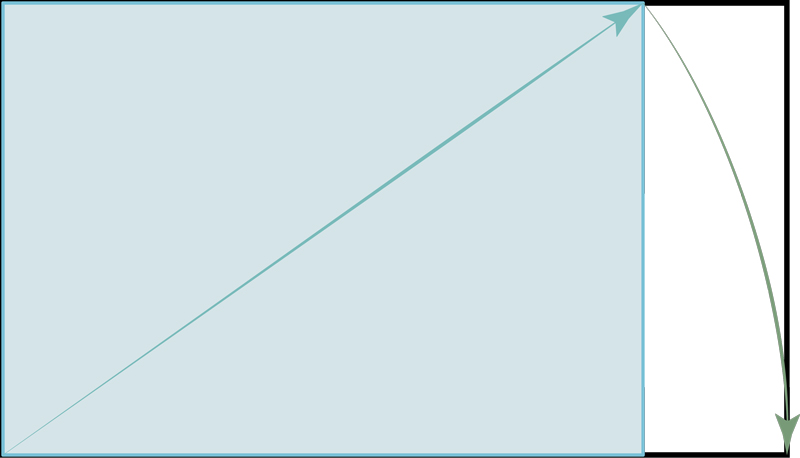
A compass swing from the diagonal of a √2 will create a √3 rectangle with the ratio of 1:1.732…  Diagram 1 & 2

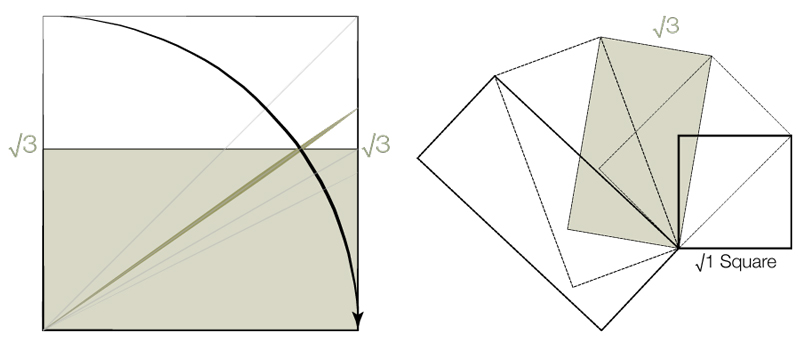
and will divide into 3 equal and proportional parts. Diagram 3

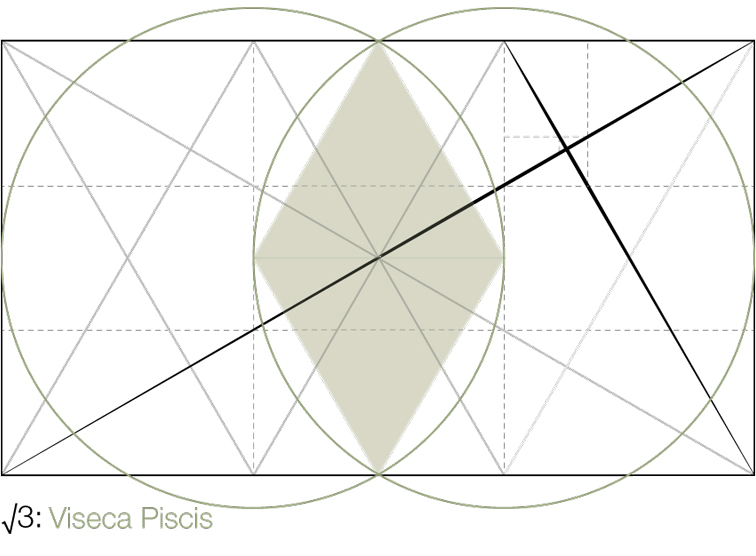
Further, the intersection of 2 circles, with the same radius, fits within the center √3 rectangular subdivision and can be divided by 2 equilateral triangles. The intersection where the circles overlap is called the Vesica Piscis which translates from Latin to Fish Bladder. Diagram 4

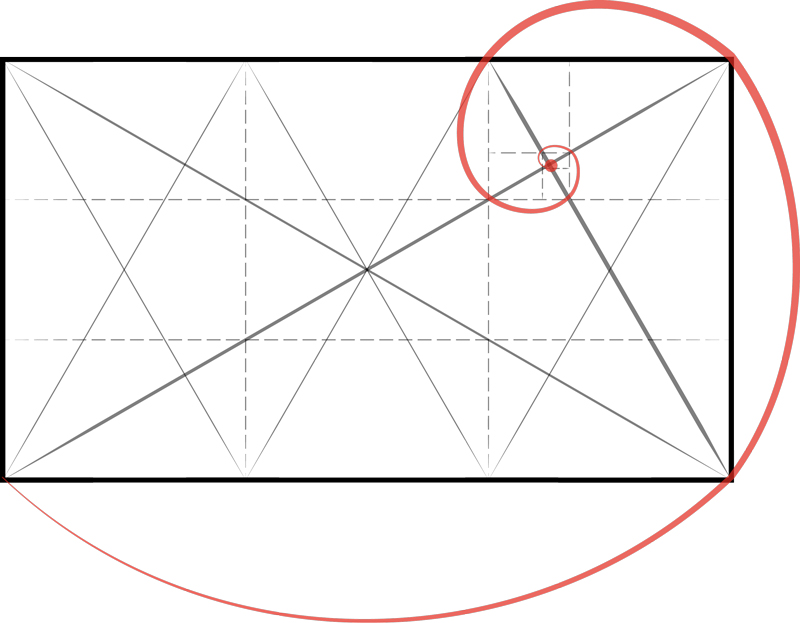
Here are two √3 logarithmic spirals. Diagram 5

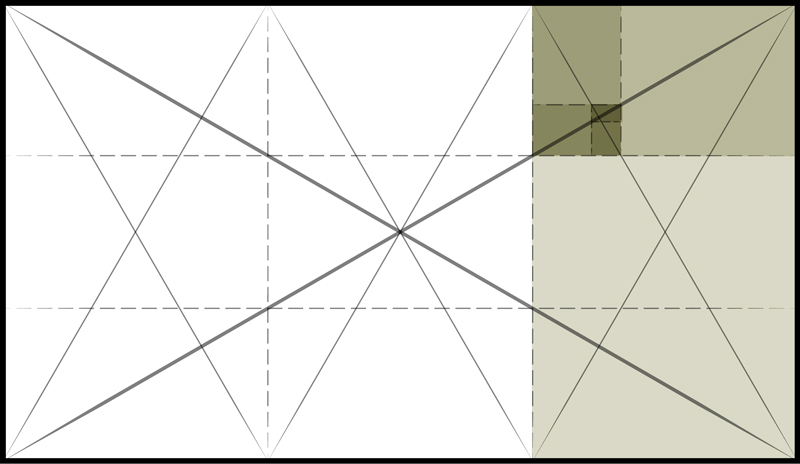
The √3 can also be divided with a square. Placing a square, equal to the short side of the √3, in the center of the √3 rectangle leaves 2 rectangles on either side that can be subdivided by another square and √3 rectangle. Diagram 6

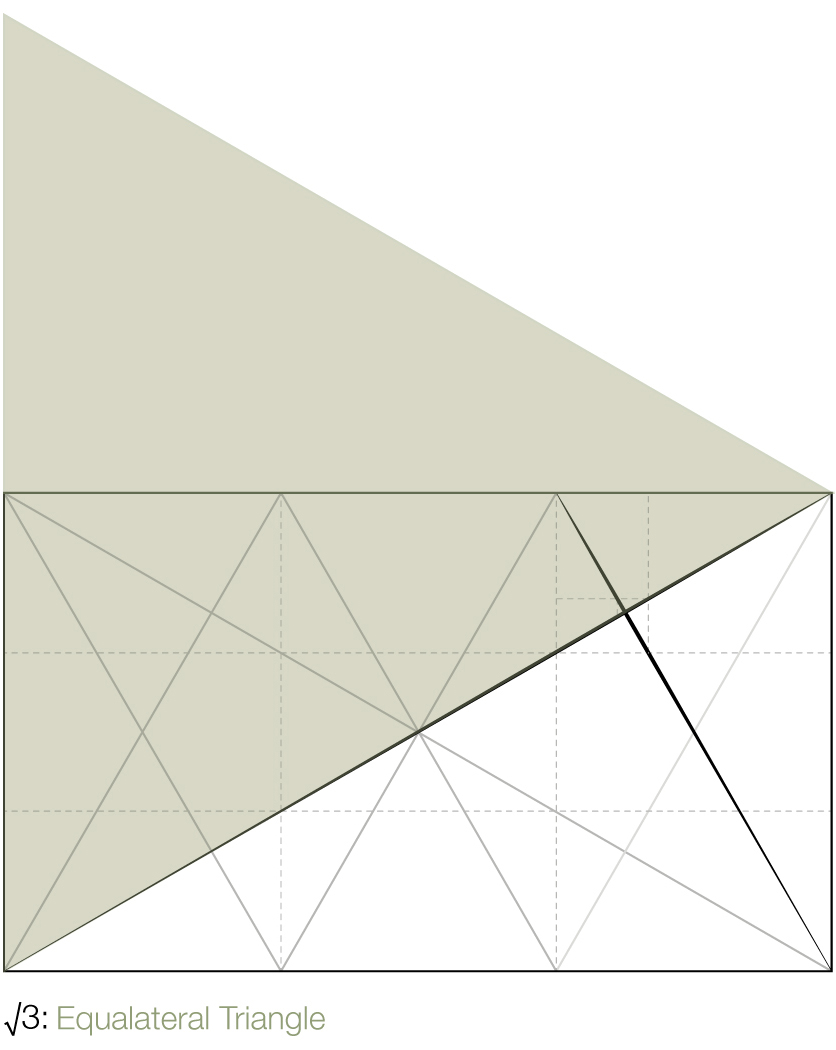
Finally, the triangle formed from the hypotenuse of the √3 will form an Equilateral triangle when mirrored about the base.* Diagram 7

Here are some examples from history. Diagram 8

*1 + 1 = 2  = √4…