We’ve spent considerable energy looking at design in painting. All of it from work created decades or centuries ago, until now.
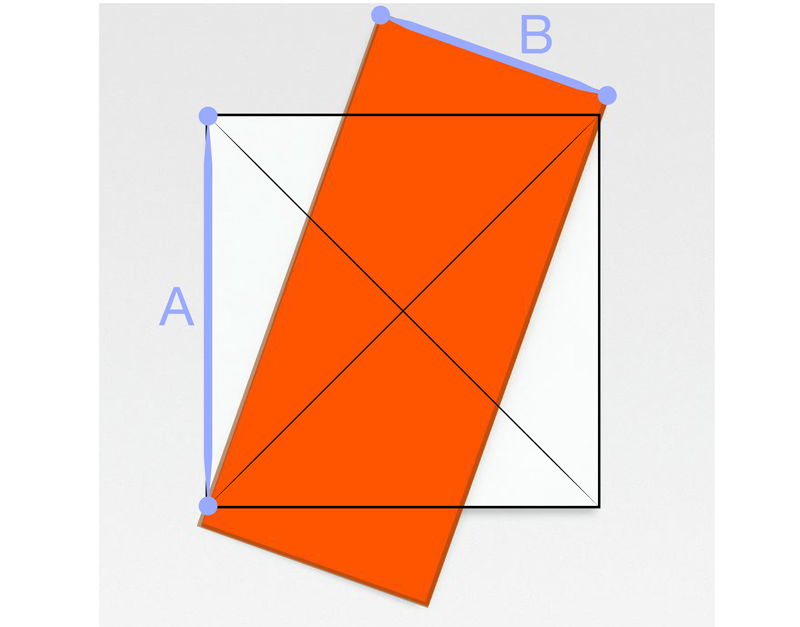
This is ‘Orange Diagonal’ by Ellsworth Kelly from 2008. Plate 1
It’s composed of two painted canvases. An orange rectangle, placed on a white square, diagonally. Seems pretty simple right? Insert my kid could do that quote.

Well, let’s take a closer look. We can see from this that the orange rectangle is actually a √5 rectangle. Plate 2

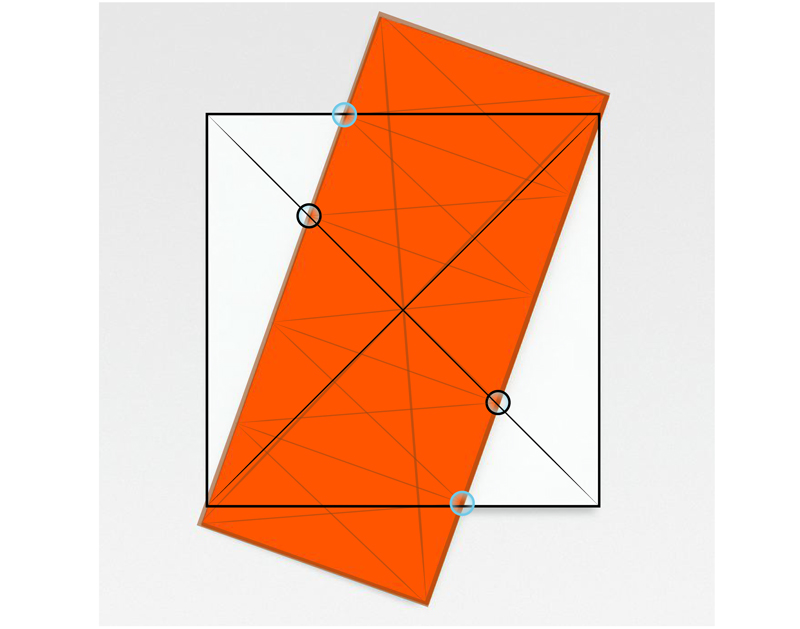
Now let’s look at all the coincidental geometry between the rectangle and the square. Plate 3
Blue Circle– The top & bottom of the square coincide with the outer 5th divisions.
Black Circle- The primary diagonal of the square coincides withe the 2nd, 5th division of the primary diagonal. Or, they coincide with the center 5th division.
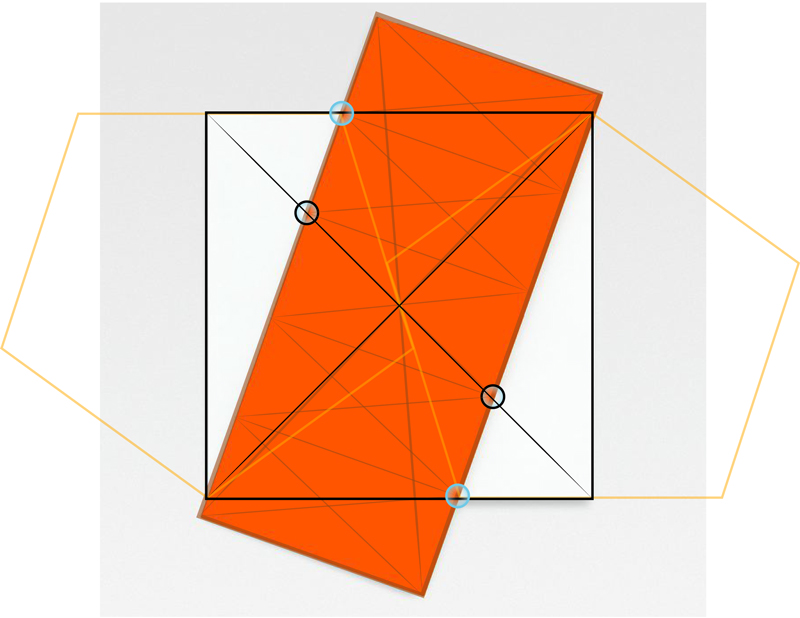
It also happens that we can use the ‘Blue Circle’ coincident and the corners of the square to construct a Pentagon. Plate 4
Since we know that every pentagon has the elements of a pentagram. Plate 5 And we also know that both the pentagram and the √5 rectangle relate to the ϕ ratio.
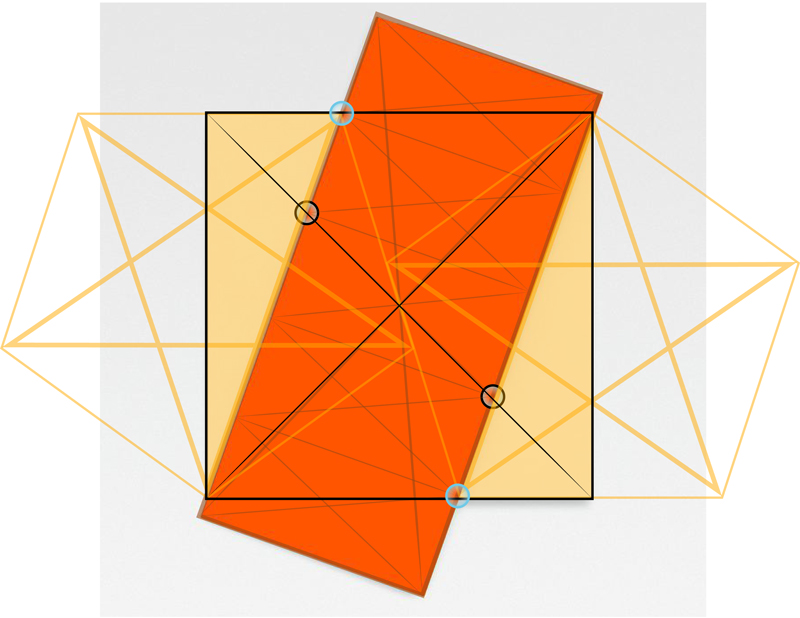
The triangles, highlighted in yellow, are each half a Φ Triangle*
The negative is just as important as the positive.
– Ellsworth Kelly
Sometimes things that seem simple are considerably more complex. Maybe even elegant?
* We’ll look at this more in the future.
Addendum- It also turns out that the ratio of the length of the square (A) to the short side of the √5 rectangle (B) is 1:0.617 which is very close to the Φ ratio. Plate 6