Nicolas Poussin finished painting ‘A Dance to the Music of Time’ in 1636. The aspect ratio of the painting is 1:1.261 (when you average the difference between the imperial and metric measurements). Plate 1

A while back we looked at ‘Triumph of Bacchus’ by Michaelina Wautier where we introduced the √ϕ. This is the explanation promised at that time.
You’ll recall from this post that the ϕ aspect ratio is 1:1.618… which continues on infinitely as an irrational number. Plate 2
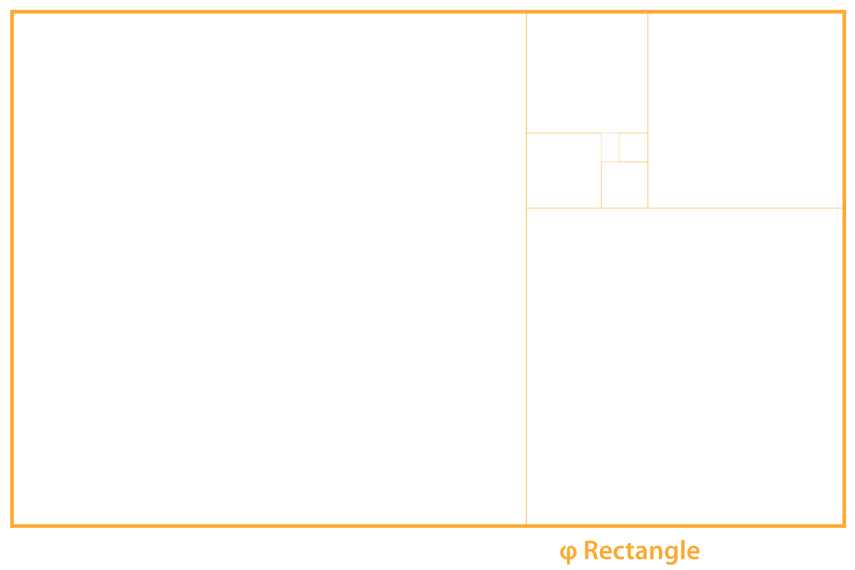
Well, the √ϕ (√1.618…) equals 1.272… which is also an irrational number. The √ϕ Rectangle has an aspect ratio of 1:1.272…
We can construct a √ϕ reciting from a ϕ rectangle by using the base (1) as the radius and swinging the compass up (2) to the top of the ϕ rectangle and then drawing a perpendicular line down from the intersection of the arc and the top of the ϕ rectangle to the base of the ϕ rectangle (3). Plate 3
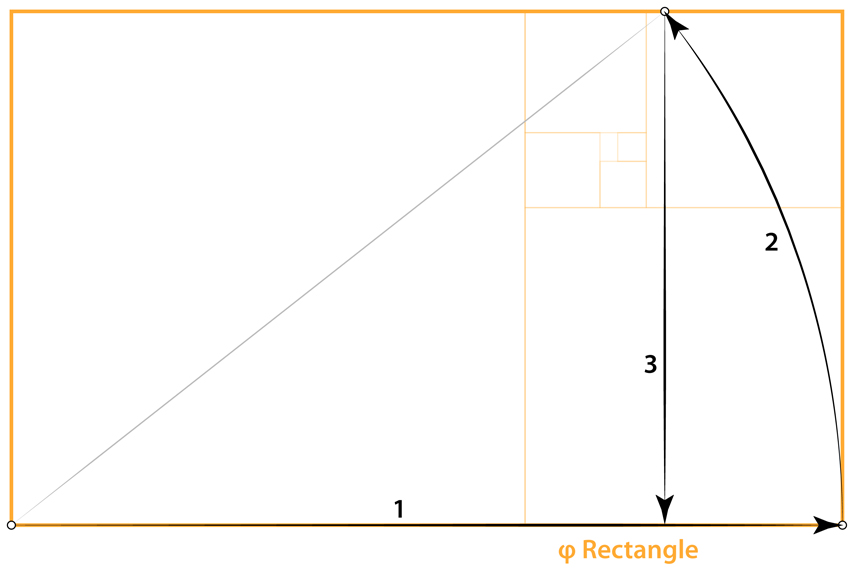
The aspect ratio of this new rectangle (shaded in gray) is the √ϕ or 1:1.272… Plate 4

The √ϕ Rectangle has primary diagonals each with two reciprocals. Plate 5
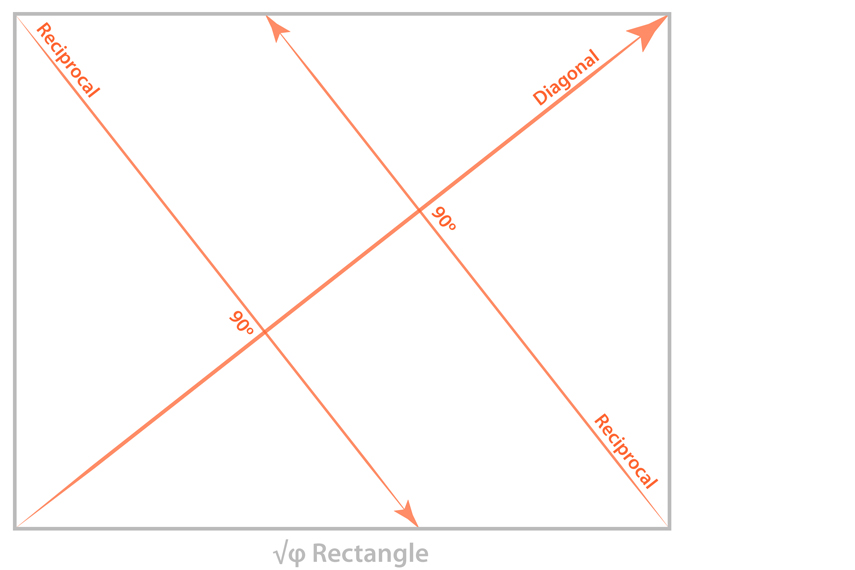
Mirroring the diagonal and reciprocals about either centerline will create the following Dynamic Symmetry armature. Plate 6

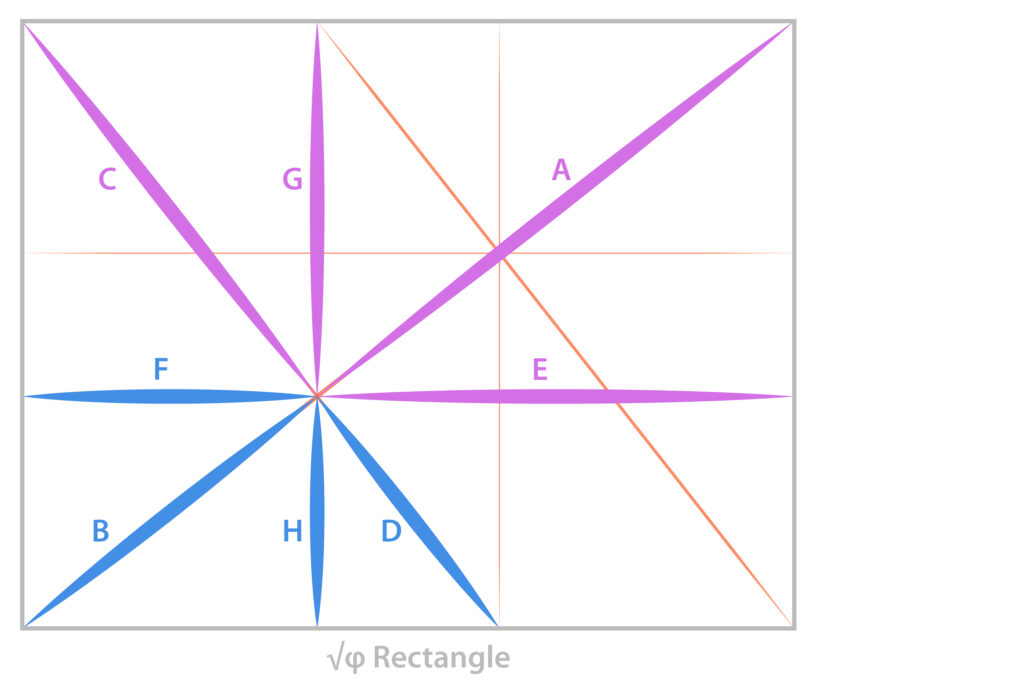
This is the same armature with vertical and horizontal subdivisions. Plate 7

One quality of the √ϕ Rectangle is that its subdivisions also have the ϕ proportions in that if the Purple Segment=1 then the Blue Segment=.618… for each of the straight line segments below. Or, A:B = C:D = E:F = G:H. Plate 8
Go back and look at ‘Triumph of Bacchus’ before we continue on to ‘A Dance to the Music of Time’ by Poussin.
The idea of beauty does not descend into matter unless this is prepared as carefully as possible. This preparation consists of three things: arrangement, measure, and aspect or form…
-Nicolas Poussin
