Some rectangles are more fun than others, mathematically, especially for design.  They are known as the Root Rectangles or the Golden Section Series.  They are special because their proportions are such that the primary diagonals and reciprocals divide the rectangles into equal sections like fractals.  Fractal Geometry is considered a recent discovery but the Square Roots and the elegance of their geometry have been understood for thousands of years.

Remember, we call the Circle, Square and Triangle primary because they are indivisible.  They represent Unity, the whole, they are complete.

Let’s begin. A square has the proportions 1:1.  The √1=1.  Easy enough.  However, the diagonal of a square happens to equal the √2 which is 1.414… (it’s an irrational number that continues on like π). We can construct a √2 rectangle by drawing a square and using it’s diagonal to swing a compass down (or up) to an adjacent side. Diagram 1

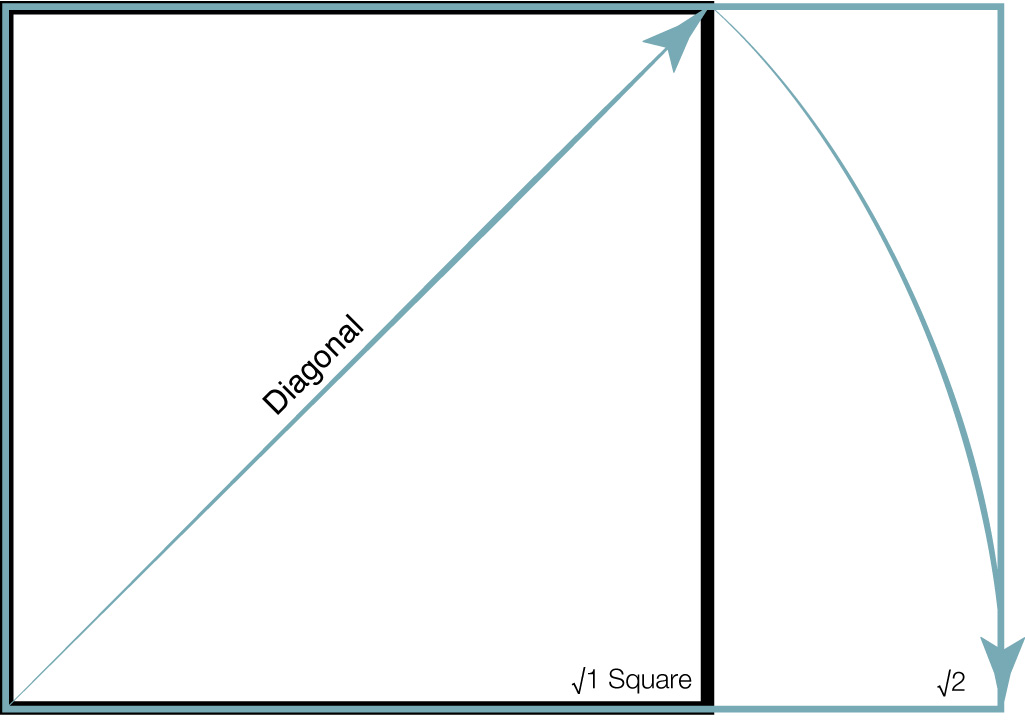
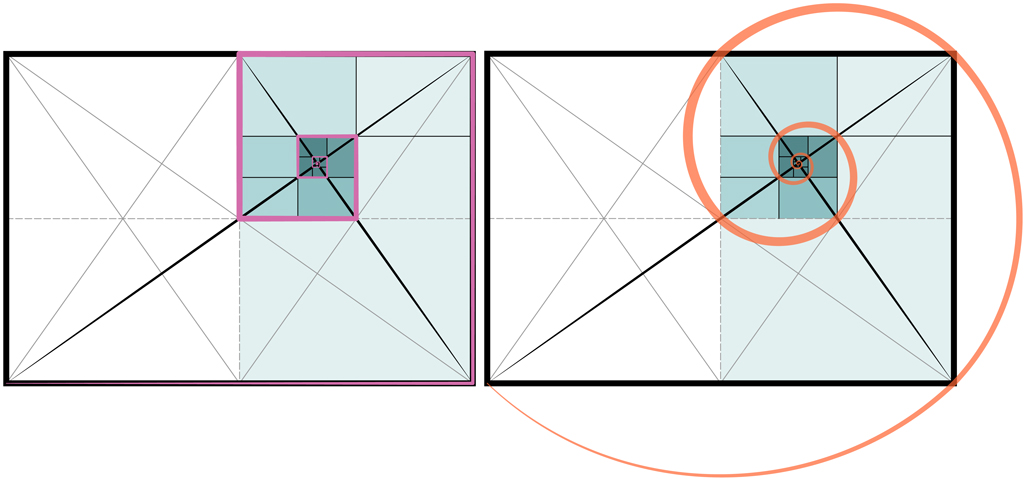
This new rectangle will have the proportions of 1:1.414. Further, we will find that it’s reciprocals will divide the parent rectangle into 2 equal child rectangles each of which has the exact same proportions as the parent 1:1.414.*

Diagram 2

Note- All rectangles that share the same diagonal are the same proportion.

The √2 has a binary subdivision by splitting the larger rectangle into 2 equal smaller, related, rectangles. As mentioned above, there are other rectangles that share similiar properties. Here’s a hint. They all relate. Diagram 3.

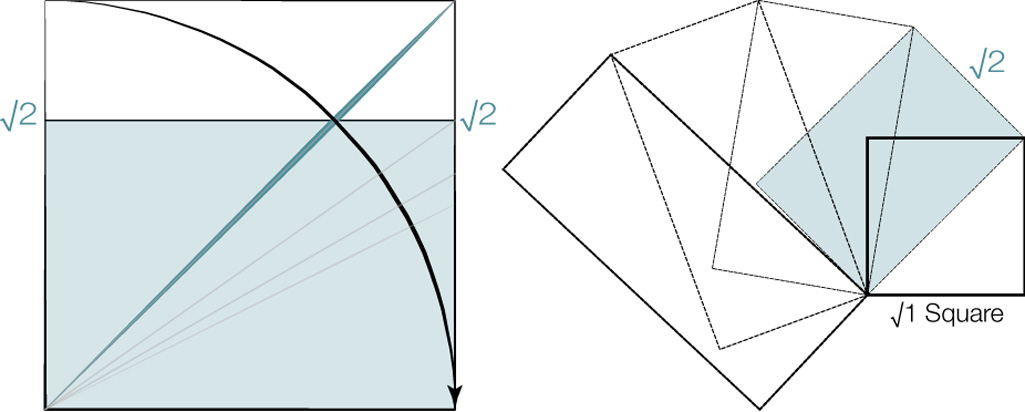
Logarithmic spirals can be formed by following the long side of each subdivision.*  Diagram 4

About now you might be thinking this…

So you may not be interested in all this math. Fair enough, what do you think of this?

Now take a look at this…

Also, see how a young Picasso use √2 the here…

*The entire rectangle adheres to these subdivisions. The diagrams shown can be rotated or mirrored to the same effect.